Skip to main content

Introduction

GEMM, General Matrix Multiplication.

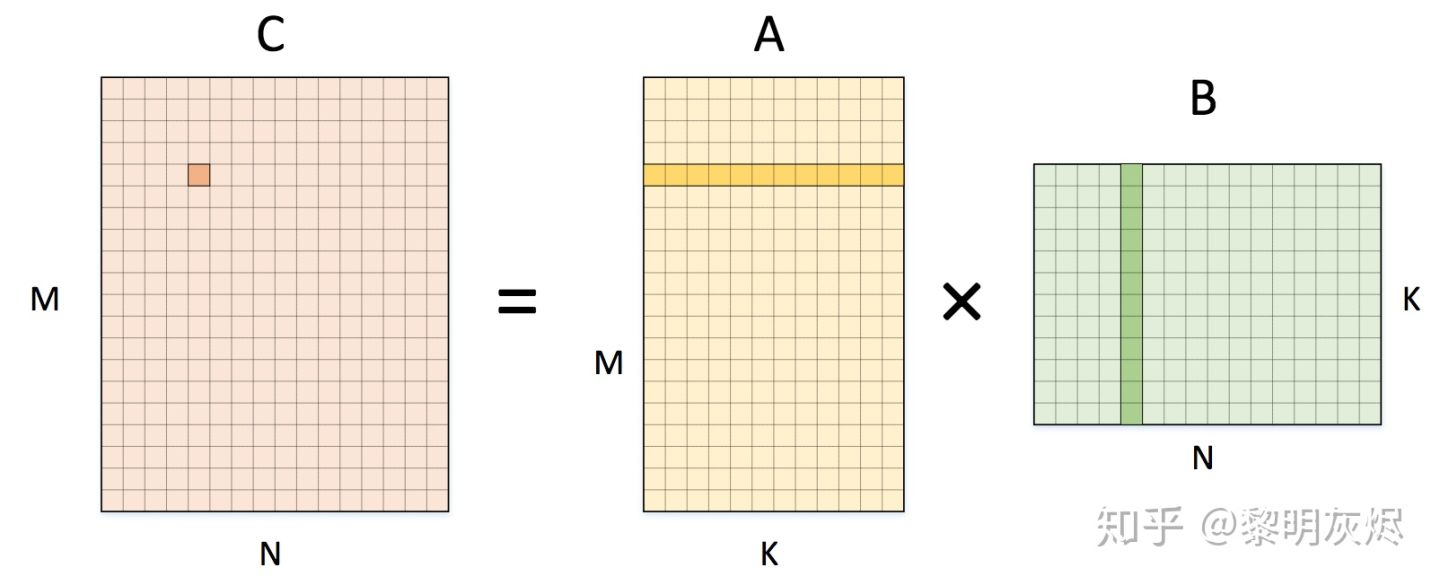C=AB; A,B,C∈Rn×nCm,n=∑k=1KAm,kBk,n;  m,n,k∈Rn\begin{align} \mathbf{C}&=\mathbf{A}\mathbf{B}; \space \mathbf{A},\mathbf{B},\mathbf{C} \in R^{n \times n} \\ C_{m,n}&=\sum_{k=1}^{K}A_{m,k}B_{k,n};\ \ m,n,k \in R^{n} \end{align}

伪代码 O(n3)O(n^3)：

for (int m = 0; m < M; m++) { // spatial axis
    for (int n = 0; n < N; n++) { // spatial axis
        C[m][n] = 0;
        for (int k = 0; k < K; k++) { // reduction axis
            C[m][n] += A[m][k] * B[k][n];
        }
    }
}

优化思路：

  • 基于算法分析的方法：根据矩阵乘计算特性，从数学角度出发，典型算法包括 Strassen 算法和 Coppersmith-Winograd 算法
  • 基于软件优化的方法：根据计算机存储系统的层次结构特性，选择性的调整计算顺序，主要有循环拆分、向量化、内存重排等

基于算法分析的方法

Strassen 算法 O(nlog⁡27)O(n^{\log_{2}7})​

  1. 分治：
    A=[A1,1A1,2A2,1A2,2],B=[B1,1B1,2B2,1B2,2],C=[C1,1C1,2C2,1C2,2]\mathbf{A} = \begin{bmatrix} \mathbf{A}_{1,1} & \mathbf{A}_{1,2} \\ \mathbf{A}_{2,1} & \mathbf{A}_{2,2} \end{bmatrix}, \mathbf{B} = \begin{bmatrix} \mathbf{B}_{1,1} & \mathbf{B}_{1,2} \\ \mathbf{B}_{2,1} & \mathbf{B}_{2,2} \end{bmatrix}, \mathbf{C} = \begin{bmatrix} \mathbf{C}_{1,1} & \mathbf{C}_{1,2} \\ \mathbf{C}_{2,1} & \mathbf{C}_{2,2} \end{bmatrix}
    C1,1=A1,1B1,1+A1,2B2,1C1,2=A1,1B1,2+A1,2B2,2C2,1=A2,1B2,1+A2,2B2,1C2,2=A2,1B2,2+A2,2B2,2\begin{align} \mathbf{C}_{1,1} &= \mathbf{A}_{1,1} \mathbf{B}_{1,1} + \mathbf{A}_{1,2} \mathbf{B}_{2,1} \\ \mathbf{C}_{1,2} &= \mathbf{A}_{1,1} \mathbf{B}_{1,2} + \mathbf{A}_{1,2} \mathbf{B}_{2,2} \\ \mathbf{C}_{2,1} &= \mathbf{A}_{2,1} \mathbf{B}_{2,1} + \mathbf{A}_{2,2} \mathbf{B}_{2,1} \\ \mathbf{C}_{2,2} &= \mathbf{A}_{2,1} \mathbf{B}_{2,2} + \mathbf{A}_{2,2} \mathbf{B}_{2,2} \end{align}
  2. 辅助矩阵：
    M1:=(A1,1+A2,2)(B1,1+B2,2)M2:=(A2,1+A2,2)B1,1M3:=A1,1(B1,2−B2,2)M4:=A1,2(B2,1−B1,1)M5:=(A1,1+A1,2)B2,2M6:=(A2,1−A1,1)(B1,1+B1,2)M7:=(A1,2−A2,2)(B2,1+B2,2)\begin{align} \mathbf{M}_{1} &:=\left(\mathbf{A}_{1,1}+\mathbf{A}_{2,2}\right)\left(\mathbf{B}_{1,1}+\mathbf{B}_{2,2}\right) \\ \mathbf{M}_{2} &:=\left(\mathbf{A}_{2,1}+\mathbf{A}_{2,2}\right) \mathbf{B}_{1,1} \\ \mathbf{M}_{3} &:=\mathbf{A}_{1,1}\left(\mathbf{B}_{1,2}-\mathbf{B}_{2,2}\right) \\ \mathbf{M}_{4} &:=\mathbf{A}_{1,2}\left(\mathbf{B}_{2,1}-\mathbf{B}_{1,1}\right) \\ \mathbf{M}_{5} &:=\left(\mathbf{A}_{1,1}+\mathbf{A}_{1,2}\right) \mathbf{B}_{2,2} \\ \mathbf{M}_{6} &:=\left(\mathbf{A}_{2,1}-\mathbf{A}_{1,1}\right)\left(\mathbf{B}_{1,1}+\mathbf{B}_{1,2}\right) \\ \mathbf{M}_{7} &:=\left(\mathbf{A}_{1,2}-\mathbf{A}_{2,2}\right)\left(\mathbf{B}_{2,1}+\mathbf{B}_{2,2}\right) \end{align}
  3. 结合：
    C1,1=M1+M4−M5+M7C1,2=M3+M5C2,1=M2+M4C2,2=M1−M2+M3+M6\begin{align} \mathbf{C}_{1,1} &=\mathbf{M}_{1}+\mathbf{M}_{4}-\mathbf{M}_{5}+\mathbf{M}_{7} \\ \mathbf{C}_{1,2} &=\mathbf{M}_{3}+\mathbf{M}_{5} \\ \mathbf{C}_{2,1} &=\mathbf{M}_{2}+\mathbf{M}_{4} \\ \mathbf{C}_{2,2} &=\mathbf{M}_{1}-\mathbf{M}_{2}+\mathbf{M}_{3}+\mathbf{M}_{6} \end{align}

Coppersmith-Winograd 算法 O(n2.376)O(n^2.376)​

基于软件优化的方法

矩阵乘的计算操作总数为 2MNK2MNK，内存访问总数为 (2+1+1)MNK=4MNK(2 + 1 + 1)MNK=4MNK，对于矩阵 C 必须要先读取内存，累加完毕后再存储（忽略了对 C 初始化的操作）。

计算拆分​

拆分为 1✖️4的小块： 

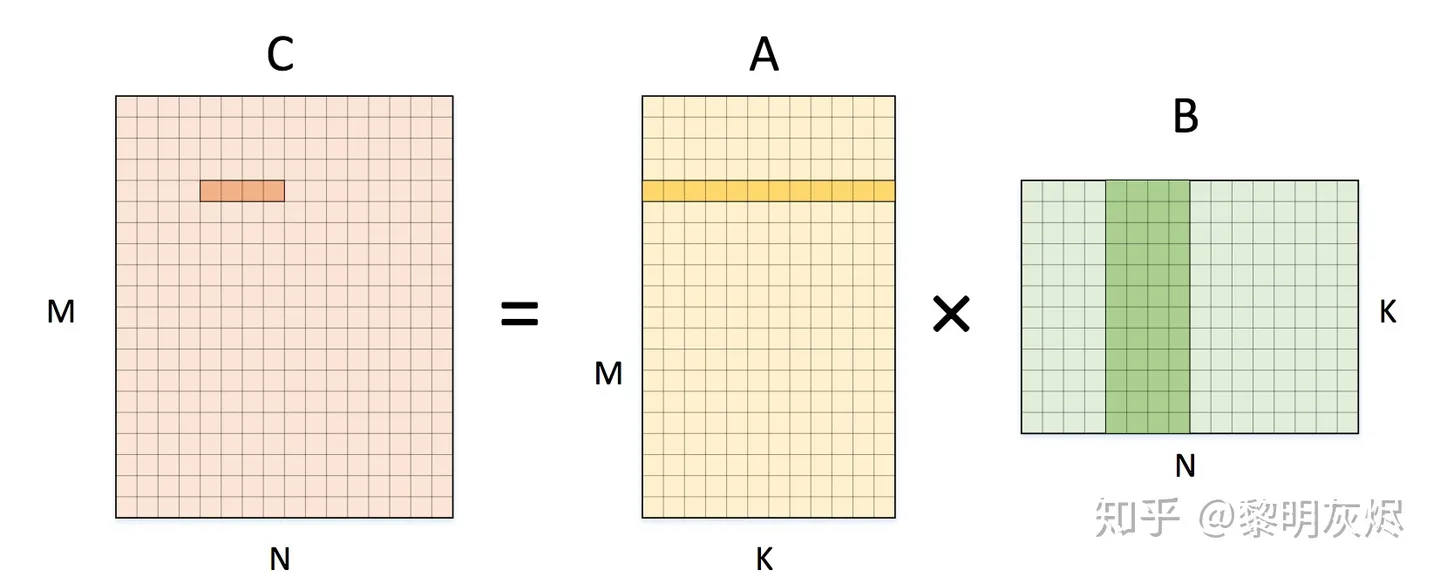
for (int m = 0; m < M; m++) {
    for (int n = 0; n < N; n+=4) {
        C[m][n+0] = 0;
        C[m][n+1] = 0;
        C[m][n+2] = 0;
        C[m][n+3] = 0;
        for (int k = 0; k < K; k++) {
            C[m][n+0] += A[m][k] * B[k][n+0]
            C[m][n+1] += A[m][k] * B[k][n+1]
            C[m][n+2] += A[m][k] * B[k][n+2]
            C[m][n+3] += A[m][k] * B[k][n+3]
        }
    }
}

计算操作数没有变化：m∗n4∗k∗4∗2=2MNKm*\frac{n}{4}*k*4*2=2MNK 内存访问数也没有变化：m∗n4∗k∗4∗4=4MNKm*\frac{n}{4}*k*4*4=4MNK 但是内层循环中对 A[m][k] 有四次重复访问，可以先将他读到寄存器中，达到复用的目的。

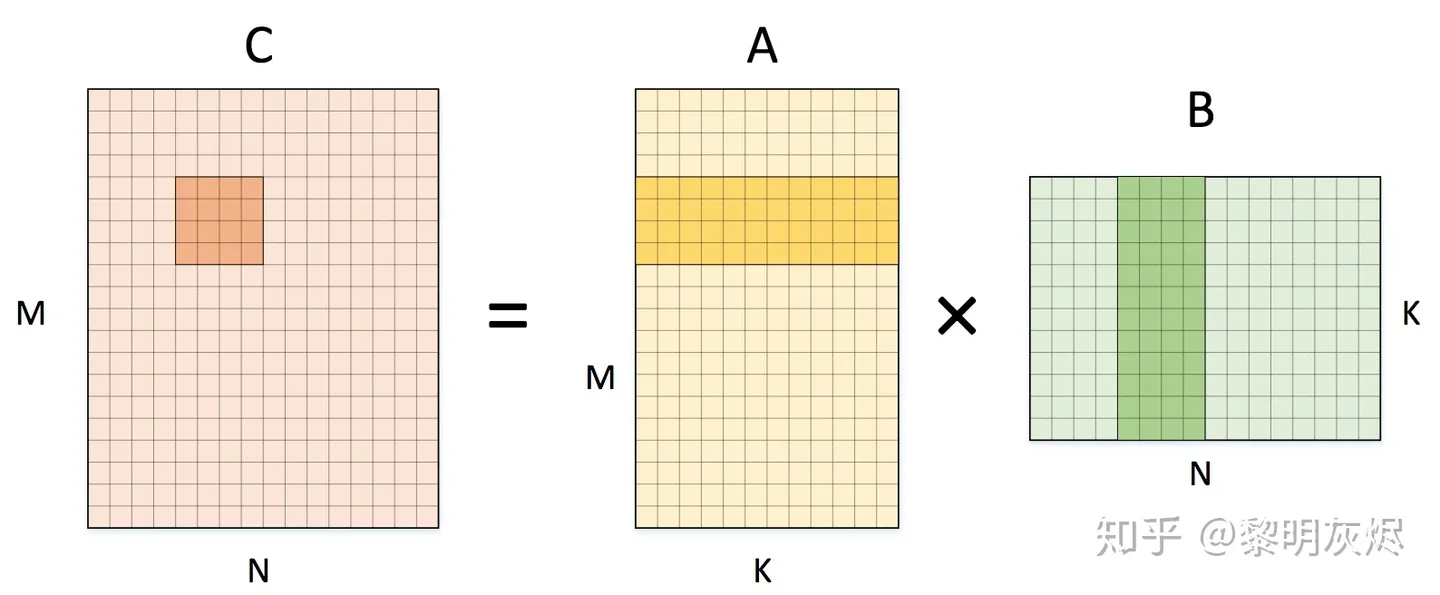
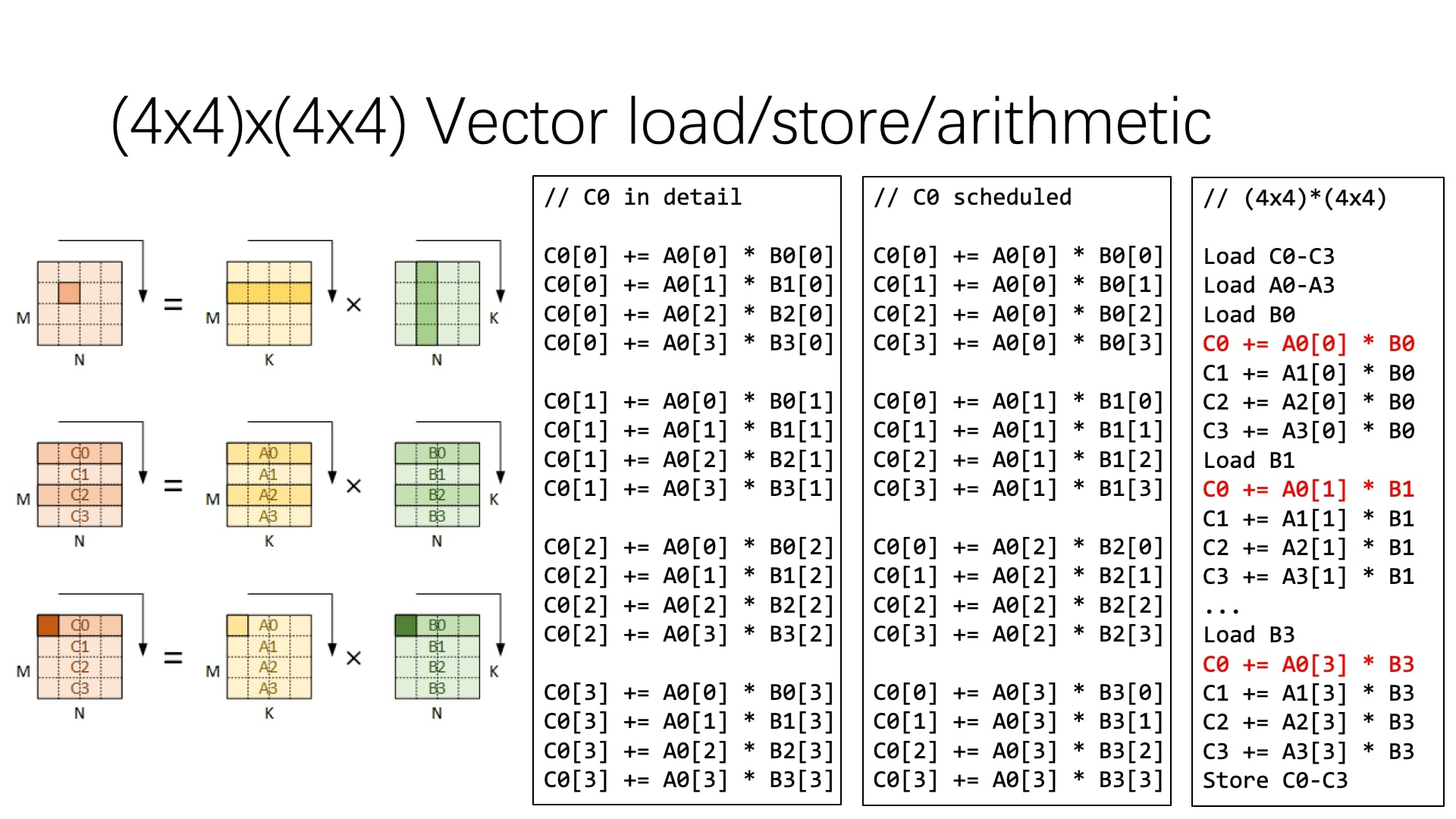
拆分为 4✖️4的小块：

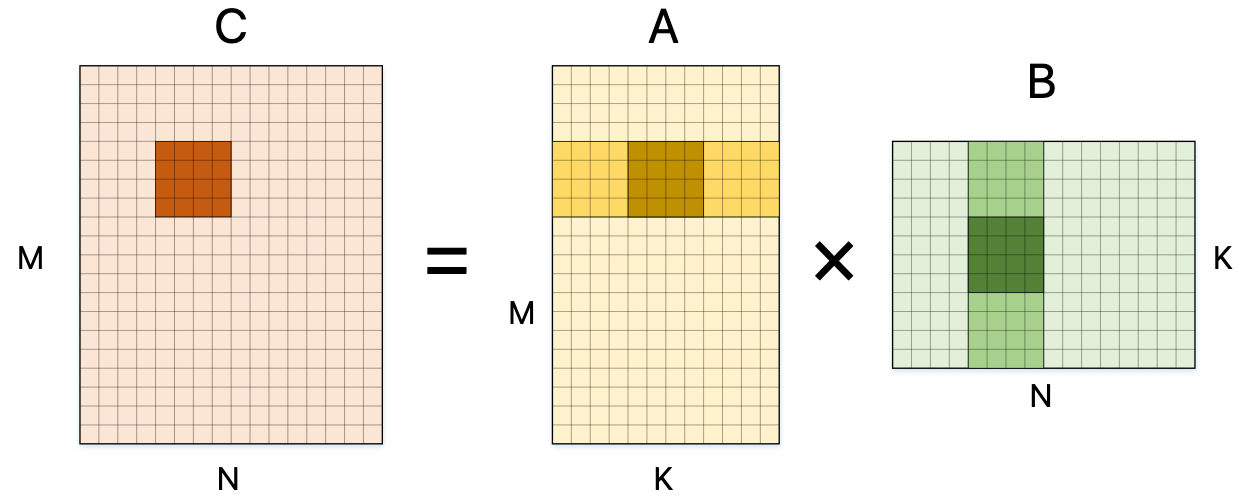
以上为针对 M, N 维度的展开，我们还可以对 K 维度进行展开：

向量化​

现代处理器有 SIMD 的能力。

内存布局的优化​

主要目的是保证缓存的命中率。 现代计算机的 cache line 一般为 64 Byte。